Determine the Set of Points at Which the Function F X Y Arctan 7x 2p Y ˆ’ 4 is Continuous

Arctan

Arctangent, written as arctan or tan^-1 (not to be confused with ) is the inverse tangent function. Tangent only has an inverse function on a restricted domain, <x<. In the figure below, the portion of the graph highlighted in red shows the portion of the graph of tan(x) that has an inverse.

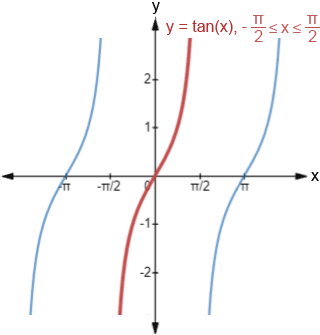
The domain must be restricted because in order for a function to have an inverse, the function must be one-to-one, meaning that no horizontal line can intersect the graph of the function more than once. Since tangent is a periodic function, without restricting the domain, a horizontal line would intersect the function periodically, infinitely many times.

One of the properties of inverse functions is that if a point (a, b) is on the graph of f, the point (b, a) is on the graph of its inverse. This effectively means that the graph of the inverse function is a reflection of the graph of the function across the line y = x.

The graph of y = arctan(x) is shown below.

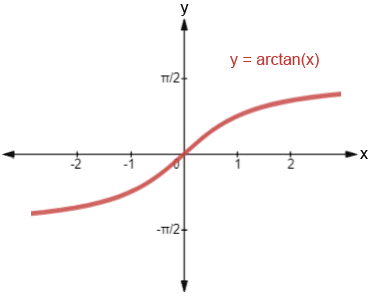
As can be seen from the figure, y = arctan(x) is a reflection of tan(x), given the restricted domain <x<, across the line y = x. The domain of arctan(x), -∞<x<∞, is the range of tan(x), and its range, <x<, is the domain of tan(x).

Arctan calculator

The following is a calculator to find out either the arctan value of a number or tangent value of an angle.

Using special angles to find arctan

While we can find the value for arctangent for any x value in the interval [-∞, ∞], there are certain angles that are used frequently in trigonometry (0°, 30°, 45°, 60°, 90°, and their multiples and radian equivalents) whose tangent and arctangent values may be worth memorizing. Below is a table showing these angles (θ) in both radians and degrees, and their respective tangent values, tan(θ).

θ	-90°	-60°	-45°	-30°	0°	30°	45°	60°	90°
tan(θ)	undefined		-1		0		1		undefined

To find tan(θ), we either need to just memorize the values, or remember that tan(θ)= , and determine the value for tan(θ) based on the sine and cosine values, which follow a pattern that may be easier to memorize. Refer to their respective pages to view a method that may help with memorizing sine and cosine values.

Once we've memorized the values, or if we have a reference of some sort, it becomes relatively simple to recognize and determine tangent or arctangent values for the special angles.

Example:

Find arctan() and arctan(-1).

, .

, .

Inverse properties

Generally, functions and their inverses exhibit the relationship

f(f^-1(x)) = x   and   f^-1(f(x)) = x

Given that x is in the domain of the function. The same is true of tan(x) and arctan(x) within their respective restricted domains:

tan(arctan(x)) = x, for all x

and

arctan(tan(x)) = x, for all x in (, )

These properties allow us to evaluate the composition of trigonometric functions.

Composition of arctangent and tangent

If x is within the domain, evaluating a composition of arctan and tan is relatively simple.

Examples:

Composition of other trigonometric functions

We can also make compositions using all the other trigonometric functions: sine, cosine, cosecant, secant, and cotangent.

Example:

Find sec(arctan()).

Since is not one of the ratios for the special angles, we can use a right triangle to find the value of this composition. Given arctan() = θ, we can find that tan(θ) = . The right triangle below shows θ and the ratio of its opposite side to its adjacent side.

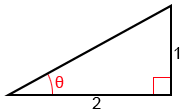
To find secant, we need to find the hypotenuse since sec(θ)=. Let c be the length of the hypotenuse. Using the Pythagorean theorem,

1² + 2² = c²

5 = c²

c =

We know that arctan() = θ, so we can rewrite the problem and find sec(θ) by using the triangle we constructed above and the fact that sec(θ) = :

sec(arctan()) = sec(θ) =

The same process can be used with a variable expression.

Example:

Find sin(arctan(3x)).

Given arctan(3x) = θ, we can find that tan(θ) = and construct the following triangle:

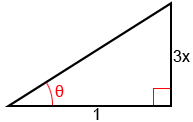
To find sine, we need to find the hypotenuse since sin(θ)=. Let c be the length of the hypotenuse. Using the Pythagorean theorem,

(3x)² + 1² = c²

9x² + 1 = c²

c =

and

sin(arctan(3x)) = sin(θ) =

Using arctan to solve trigonometric equations

Arctangent can also be used to solve trigonometric equations involving the tangent function.

Examples:

Solve the following trigonometric equations for x where 0≤x<2π.

1. 3tan(x) =

3tan(x) =

tan(x) =

x = arctan()

Tangent is positive in two quadrants, quadrants I and III, so there are two solutions: x = and x = . These are the only two angles within 0≤x<2π whose tangent value is equal to .

2. tan²(x) - tan(x) = 0

tan²(x) - tan(x) = 0

tan(x)(tan(x) - ) = 0

tan(x) = 0 or tan(x) - = 0

tan(x) = 0 or tan(x) =

x = 0, π or x =

alexandercathery.blogspot.com

Source: https://www.math.net/arctan

Share this post